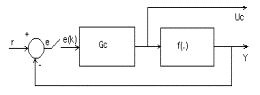
Şekil 1 Sayısal arama probleminin, bir otomatik kontrol sistemi olarak görülmesi.
GLOBAL OPTİMİZASYON |
* Global Optimizasyon Teorisi * Optimizasyon yazılımları (CRS, Genetik, Bulanık)
|
Özet : Burada geliştirilen sayısal kontrol tekniği ile, çok değişkenli lineer olmayan amaç ölçüt fonksiyonlarının global optimizasyonu amaçlanmaktadır. Geri beslemeli bir kontrol sisteminde, kontrol edilen sistemi temsil eden diferansiyel denklem takımı yerine lineer olmayabilen bir f(x) fonksiyonu yerleştirildiğinde uygun tasarlanmış kontrolör çıkışı, sürekli halde , f(x)-r=0 ile ifade edilen denklemin çözümünü verir. Bu çalışmada verilen global optimizasyon tekniğinde bulanık mantık ile çalışan ayrık sayısal kontrolör ve değişken referans işaretleri kullanılmaktadır. Amaç ölçüt fonksiyonunun çözüm aralığının alt ya da üst sınırındaki değerleri referans alınarak kök arama işlemi gerçeklenir. Her kök arama işleminden sonra referans işaret arttırılır ve kontrolör çıkışı diğer parametre sınırına erişinceye kadar bu işleme devam edilir. Doymaya erişmeden önceki bulunan son kök değeri global ekstremum olarak alınır.
I. Giriş
f*=min f (x) , x ÎX
(1)
şeklinde tanımlanan f* değerini bulmayı amaçlar . f(x)
fonksiyonunu minimize eden x değeri, ayrıca f(x)
fonksiyonunu maksimize ettiğinden, bu tanım global maksimum için de geçerlidir
ve genel olarak global optimizasyon problemi olarak adlandırılır. Amaç ölçüt fonksiyonu fnin süreksizliliği,
birden fazla ekstremumu bulunması, kullanılacak optimizasyon tekniğini kısıtlar.
Örneğin, süreksiz bir amaç ölçüt fonksiyonunun optimizasyonunda, türev ifadesini kullanan yöntemlerde sorunlarla karşılaşılır.
Şekil 1de birim geribeslemeli bir ayrık kontrol sisteminin blok yapısı görülmektedir. f(.) diferansiyel denklem takımı yerine bir f(x) fonksiyonu konması halinde, kontrol kuramı kullanılarak, (1) ile tanımlanan global optimizasyon probleminin çözümüne,aynı blok diyagramı ile yaklaşılabilir.

Şekil 1 Sayısal arama probleminin, bir otomatik kontrol sistemi olarak görülmesi.
k®¥ için e(k)®0, f(Uc(k))®r (2)
ya da, * optimum çözümü ifade etmek üzere,
f(Uc)-r ½®0 ? Uc*=x* , f(x*)=r (3)
k®¥
ifadeleri geçerlidir.
Buna göre, Uc kontrolör çıkışı, f(x)-r=0 denkleminin çözümünü verir. Özel olarak referans işaretinin r=0 olarak verilmesi durumunda , sürekli halde Ucnin son değeri, f(x) fonksiyonunun bir köküne karşı düşer. Bu kontrol kuramı yaklaşımı diferansiyel denklemlerin nümerik çözümlerinde optimum adım boyunun hesaplanmasında kullanılmıştır[1] . Bu çalışmada ise, aynı yaklaşım, global optimizasyon probleminin çözümünde kullanılacak olan bir fonksiyonun köklerinin belirlenmesinde kullanılmıştır.
Şekil 2de önerilen kapalı çevrim kontrol düzeni ile f(x)-r=0 denkleminin çözümü elde edilir. Burada örnekleme periyodu k adım sayısına karşı düşmekte ve çözüm olarak kontrolör çıkışı değerlendirilmektedir. Denklemlerin nümerik yöntemlerle özyinelemeli çözümleri yerine kontrol kuramı yaklaşımı ile çözümünde klasik kontrolörlerin kullanımı bazı sorunlar getirmektedir. Örneğin kök arama probleminde, PID türü kontrolör kullanıldığında, çözüme erişmede kararlılık sorunları ile karşılaşılmıştır. Çözümü aranan f(x) fonksiyonunun kök civarındaki türevinin büyük olması sadece salınım yaratmamakta aynı zamanda kök noktasının atlanmasına da sebep olabilmektedir.
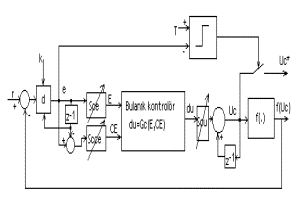
Burada açıklanann çözüm tekniğinde Mamdaninin [4] önerdiği bulanık kontrolör yapısı kullanılmıştır. Şekil 2de görülen blok yapıda e hatayı, ce hata değişimini, Sce hata ölçeklendirilme katsayısını, Scce hata değişiminin ölçeklendirilme katsayısını, E ölçeklendirilmiş hatayı, CE ölçeklendirilmiş hata değişimini, du bulanık kontrolör çıkışını,Uc ayrık integre edilmiş kontrolör çıkışını ve Uc* ulaşılan kök değerinin göstermektedir.
Bu tür bir bulanık kontrolörün du çıkışı, hata ve hatanın değişimine göre belirli bir karar değerinden sonra doymaya girmektedir. f(x) fonksiyonu kökünün aranmasında kullanılan kapalı çevrimli sistemdeki tek bellek elemanı bulanık kontrolör çıkışındaki integratördür. Nümerik çözüm amaçlı bu sistem, sınırlı giriş için sınırlı çıkış üreteceğinden, yanlış kontrolör parametresi seçimi, yanlızca aranan kök civarında sınırlı genlikli salınıma yol açmaktadır. Bulanık kontrolör karar tablosu doğru seçilmiş ise, giriş kazanç parametrelerinde (Sce, Scce) ideal değerden sapma olması durumunda bile,sistem en fazla aranan kök civarında kararlı bir osilasyona girer. Bulanık kontrolör çıkışı Uc, her iki işaret yönünde de doymaya girdiğinden sistem en azından Lyapunov anlamında kararlıdır. Arama yapılan bölgede kök yoksa ya da ilk koşul olarak bulanık kontrolör çıkış kazancı, fonksiyonun Lipchitz değerine göre çok büyük ise, Uc kontrol işareti arama sınırının dışına çıkacaktır. Bu durumda arama yapılan bölgede bir kök bulunsa da bulunmasada , bölgede bir kökün bulunmadığı sonucuna varılır.
k.adım sonrasında oluşan hata,
e(k)=[r-f(Uc(k))]d (4)
ile ifade edilebilir. Burada r giriş referans işareti olup kök arama probleminde değeri sıfırdır. Başlangıç noktasına göre istenen yönde kök arayabilmek için bir defaya mahsus olmak üzere 1.adım sonunda d sabiti şu şekilde belirlenir,
ì d(0)=+1, +e(0) yönünde kök arama ? d(k>0)= +1
d= í d(0)=+1, -e(0) yönünde kök arama ? d(k>0)= -1
î (5)
ve e hata işareti, (5)le tanımlanan d sabiti ile çarpılarak istenen yönde kök aramaya devam edilir. Bulanık kontrolör karar mekanizması için gerekli olan hatanın değişimi,
ce(k)= (1-z-1)e(k) = e(k)-e(k-1) (6)
fark ifadesi ile elde edilir. Ölçeklendirilmiş hata E ve hatanın değişimi CE
E(k)=Sce × e(k) (7)
CE(k)=Scce × ce(k) (8)
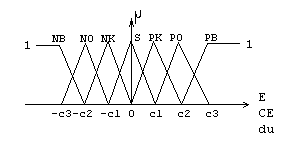
Bulanıklaştırma sonucu, E
ve CEnin üyelik dereceleri oranında aldıkları (NB, NO, NK, S, PK, PO, PB) değerlerine göre bulanık çıkış değeri,
tablo 1 ile atanmaktadır.
Tablo 1 - Hata (E) ve Hatanın değişimine (CE) göre bulanık karar tablosu
E CE |
NB |
NO |
NK |
S |
PK |
PO |
PB |
NB |
NB |
NB |
NB |
NB |
NO |
NK |
S |
NO |
NB |
NB |
NB |
NO |
NK |
S |
PK |
NK |
NB |
NB |
NO |
NK |
S |
PK |
PO |
S |
NB |
NO |
NK |
S |
PK |
PO |
PB |
PK |
NO |
NK |
S |
PK |
PO |
PB |
PB |
PO |
NK |
S |
PK |
PO |
PB |
PB |
PB |
PB |
S |
PK |
PO |
PB |
PB |
PB |
PB |
Elde edilen bulanık karar ve üyelik dereceleri, ağırlık merkezi yöntemi ile durulanarak du çıkış değeri elde edilmiştir.
4
Suim(ui)
i=1
du
= ____________
(9)
4
Sm(ui)
i=1
Arama yapılacak üst sınır UB ; başlama noktası LB olsun . Yapılan uygulamada ,
c3=½UB/2½ , c2=(2/3)×c3 , c1=(1/3)×c3 (10)
alınmıştır. (LB,UB) aralığında arama yapabilmek için Uc(0)=LB olmalıdır. Yapılan bu atama nümerik arama işlemine istenen bir noktadan başlanmasını sağlamaktadır. Ayrık integratör çıkışı,
Uc(k)=Uc(k-1)+Scu×du(k) (11)
olacaktır. Kök araması yapılan f(x)
fonksiyonu hakkında bir ön bilgi olarak Lipchitz değeri verilmiş ise [2], (LB,UB) aralığındaki herhangi x1, x2 için,
L³½f(x1)-f(x2)½/½x1-x2½ ve ½x1-x2½³r (12)
koşulları sağlanmalıdır. Burada r arama işlemi sırasında kullanılan rakamsal en küçük çözünürlük değeridir (örneğin 0.000001 gibi).
Kök arama probleminde, köke ulaşılmış koşulu f(Uc(k))=0 anlamına geldiğinden (12)deki f(x2) değeri f(Uc(k)) olarak değerlendirilirse, (12) denklemi
Uc(k) < ½f(Uc(k-1))½/L + Uc(k-1) (13)
şeklinde ifade edilebilir ve burada kök koşulu,
f(Uc(k-1))<0 ? max(f(Uc(k-1)))=0
f(Uc(k-1))>0 ? min(f(Uc(k-1)))=0 (14)
şeklinde yazılır.
(11)deki Uc değeri (13)de yerine konulursa,
L(k)=max(L(k-1),|f(Uc(k))-f(Uc(k-1))| /|Uc(k)-Uc(k-1)|) (16)
ifadesi ile üretilebilir. Burada elde edilen L(k) değeri adım duyarlılığına karşılık düşmektedir. L(k), L değerinin bilinmediği durumda Scunun ayarlanmasında kullanılabilir fakat kuramsal olarak sonuca erişmeyi garanti etmez.
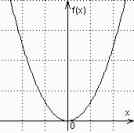
(a)
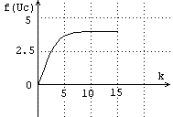
(b)
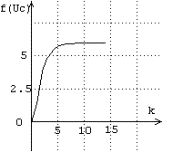
(c)
Şekil 4 a) f(x)=x2 fonksiyonu b) (0,10) aralığında f(x)-4=0 çözümü c) f(x)-6=0 çözümü
Önerilen global optimizasyon yönteminin bir parçası olan kök arama işleminin kolay anlaşılması için, ilk olarak f(x)=x2 örneği seçilmiştir. Şekil 4bde referans giriş r=4 için (0,10) aralığında k=15 iterasyonda f(Uc(15))=4 sonucuna ulaşılmıştır. Diğer bakış açısıyla, sonlandırma kriteri T=0.001 için, 15 iterasyon sonunda x2-4=0 denkleminin x=+2 noktasındaki kökü bulunmuştur. Buna karşılık T=0.0001 için çözüme 17 iterasyonda gelinmektedir. Şekil 4cde r=6 için x=0dan başlayarak, k=14 iterasyonda T=0.001 hata toleransı ile x=+2.44949daki köke ulaşılmıştır. Her iki referans işareti durumunda da Sce=0.8, Scce=0.3 , Scu=0.4 değerleri seçilmiştir.
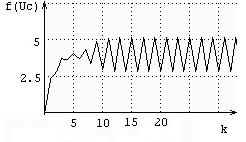
Şekil 5 r=4 için kontrolör parametrelerinin büyük seçilmesi
Unimodal bir fonksiyonun optimisazyonu ya da köklerinin bulunmasına ilişkin çok sayıda yöntem bulunmaktadır. Bilindiği üzere lokal kök arama veya optimizasyon yöntemleri unimodal olmayan fonksiyonlarda başarısız olabilmektedir. Bulanık kontrolör kullanılan bu yeni yöntemde, verilen bir başlangıç noktasından itibaren istenilen doğrultudaki bir köke erişilirken, sadece daha önceki sayısal denemeler ve bulanık karar tablosu referans alındığından, fonksiyonun karmaşıklığı çözüme ulaşma başarısını etkilemez. 3.Bölümde açıklanacağı üzere, bu özellik global optimizasyon probleminin çözümünde kullanılacaktır. Şekil 6da,f(x)=0.1x2-5+2sin(2x) fonksiyonunun (-10,+10) aralığındaki değişimi görülmektedir.
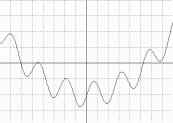
Şekil 6 (-10,10) aralığında f(x)=0.1x2-5+2sin(2x) değişimi
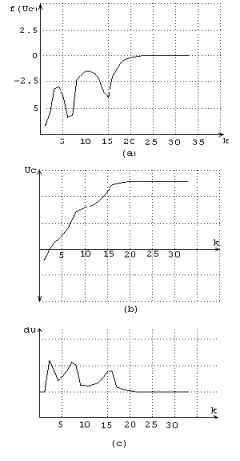
Şekil 7- r=0 için LB=Uc(0)=-1 UB=10 için
kök aramada a) Fonksiyon çıkışı f(Uc) , b)Fonksiyon giriş işareti Uc c) Bulanık kontrolör çıkışı dunun, k iterasyon sayısına göre değişimleri
Şekil 6da görülen f(x)=0.1x2-5+2sin(2x) fonksiyonunun x=-1den başlayarak sağ tarafa doğru +10 üst sınırı ile kökü aranması durumunda , Sce=0.8, Scce=0.3, Scu=0.3 için 33 çevrimde T=0.0001 hata toleransı ile x=6.48678deki köke ulaşılmaktadır.
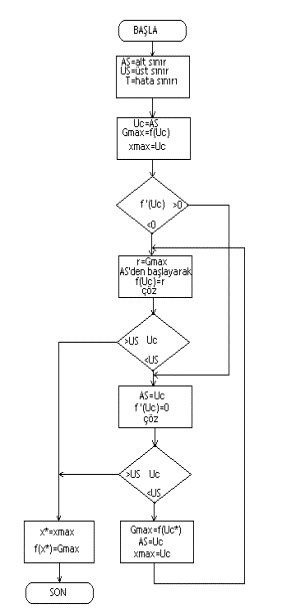
Bulanık kontrolör ile global optimizasyon için çeşitli yaklaşımlar mümkündür. Burada önerilen optimizasyon algoritması, bulanık kontrolörlü kapalı çevrim kontrol düzeni ile çözüm istenen aralığın taranması üzerinedir. Tarama işlemi, alt sınırdan üst sınıra, üst sınırdan alt sınıra, ya da çok başlangıç noktalı yapılabilir. Ek 1de görülen optimizasyon algoritması alt sınırı başlangıç noktası kabul etmekte ve verilen bir f(.) fonksiyonunun maksimum değerini aramaktadır. Aramaya başlanan noktada fonksiyon artış yönünde ise r=0 için f(Uc)=0 çözümü sağa doğru aranır ve bulunan ilk kök yeni global maksimum noktası olarak kabul edilir. Aramaya başlanan noktada fonksiyon azalma yönüde ise, r=f(Uc) için sağa doğru bulanık kontrolör ile kök aranır ve bulunan ilk kökten itibaren r=0 için f(Uc)=0 çözümü elde edilerek varılan yeni nokta global maksimum kabul edilir. Her iki halde de r=yeni global maksimum, alınarak f(Uc)=r çözümü ile tekrarlı olarak işleme devam edilir. Arama sırasında kontrol işareti Uc>UB koşulu oluşursa varılmış olan en son f(Uc)=0 çözümü global maksimumu verecektir. f(Uc)=0 çözümünde türev alma işlemini gerçekleştirmek için geri besleme yoluna z-1 öteleyici ve fark alıcı konularak f(k)-f(k-1) değeri kullanılabilir. Fakat adım boyu farklı olduğundan doğru sonuca ulaşmaktaki başarım düşmektedir. İşlem bilgisayar ortamında yapıldığında tercih edilmesi gereken, f(x) yerine sayısal türev (Örneğin (f(x+h)-f(x))/h) kullanmaktır.
f(x)=0 alt işletiminde, sonlandırma kriteri olarak global aramada istenen duyarlılığı almak gerekmez. Çünkü, global noktalara f(x)=0 çözümünün sonrasında ulaşılmaktadır. Örneğin, T=0.000001 hata üst sınırı ile çözüm isteniyorsa; kök arama çevrimlerinde T=0.01 ; türev arama çevrimlerinde ise T=0.000001 seçmek aynı doğrulukta daha kısa sürede çözüme ulaşmayı sağlayacaktır.
Optimizasyon değişkenleri üzerine getirilebilecek kısıtlamalara uymak için, amaç ölçüt fonksiyonuna ceza bileşeni eklenebildiğinden burada ayrıca ele alınmamıştır.
(a)
(b)
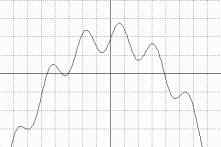
Şeril 8- a) (-10,10) aralığında f(x)=-0.2x2+5+2sin(2x) fonksiyonu b) Global maksimum aranmasında Ucnin değişimi
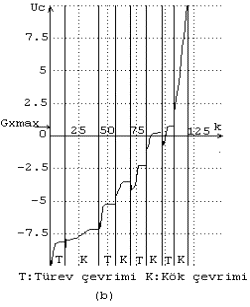
Şekil 8-ada görülen f(x)=-0.2x2+5+2sin(2x)
fonksiyonu için (-10,10) aralığında global maksimum aranmasında 10 noktası başlangıç noktası alınmıştır. f(-10)>0 olduğundan aramaya türev çevrimi ile başlanmıştır.
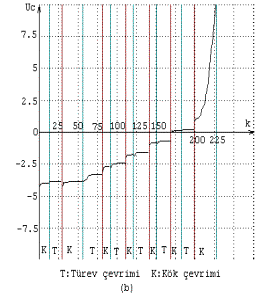
Şekil 8-bde görüleceği üzere dördüncü türev çevrimi sonunda x=0.7475016 da
global maksimum olan f(x*)=6.882506 değerine t=0.00001 hata üst sınırı ile
ulaşılmıştır. f(x*) referans alınarak yapılan bir sonraki kök
çevriminde, toplam 120 iterasyon sonunda Uc>+10 değeri ile doyma oluştuğundan işlem
sonlandırılmıştır (Şekil 8-b). Buradaki kök arama çevrimlerinde Sce=0.6, Scce=0.2,
Scu=0.3 ; türev çevrimlerinde ise Sce=0.4 , Scce=0.1 , Scu=0.2 alınarak işlem yapılmıştır.
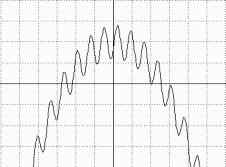
Şekil 8daki fonksiyonun frekansı arttırılmış hali olan f(x)=-0.5x2+5+2sin(7x) (Şekil 9), x=0 civarında birbirine yakın maksimumlar içerdiğinden
daha düşük ölçekleme katsayıları ile doğru sonuca erişilmektedir. Şekil 9da görüleceği
üzere global maksimum değeri olan x*=0.2220655deki f(x*)=6.975077
değerine ,x=-4 başlangıç koşulu ile, toplam 228 iterasyonda ulaşılmıştır.
Burada, T=0.00001, kök çevrimlerinde Sce=0.5, Scce=0.2, Scu=0.2 ; türev çevrimlerinde
Sce=0.4, Scce=0.1, Scu=0.05 değerleri kullanılmıştır
(a)
Şekil 9- f(x)=-0.5x2+5+2sin(7x) fonksiyonu ve global maksimum noktasının aranması
Tablo 2de, bulanık kontrolör kullanılarak global optimizasyon ile diğer bazı yöntemlerin sonuca erişimdeki yineleme sayıları görülmektedir [2]. Global optimizasyon problemlerinde yineleme sayısı, kullanılan yönteme ve optimize edilen fonksiyona bağlı olarak çok değişkenlik göstermektedir. Tablo 2de karşılaştırılması yapılan fonksiyonlar diğer yöntemlerin başarılı oldukları arasından seçilmiştir.
Tablo 2 Global minimum araması yapılan bazı test fonksiyonları ve literatürde yer alan bazı algoritmaların sonuca erişimdeki değerlendirme sayıları
f(x) |
Aralık |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
|||
f1(x) |
(2.7
, 7.5) |
57 |
29 |
45 |
462 |
120 |
|||
f2(x) |
(3.1
, 20) |
68 |
38 |
442 |
448 |
158 |
|||
f3(x) |
(-10
, 10) |
159 |
165 |
150 |
3817 |
816 |
Tablo 2de yer alan fonksiyonlar,
f1(x)= sinx+sin(10x/3)+lnx-0.84x
f2(x)= sinx+sin2x/3
5
f3(x)= -Ssin((i+1)x+i)
i=1
ve karşılaştırma yapılan yöntemler aşağıda sıralanmıştır.
Y1=Bulanık kontrolör
Y2=Zilinskas 2
Y3=Strong
Y4=Pijav
Y5=Batish
IV. Sonuç
Burada önerilen global optimizasyon yönteminde, f(x) için bir Lipchitz değeri verilebilmesi durumunda çözümün doğruluğu garanti edilir.Fonksiyonun süreksiz olması durumunda, kuramsal olarak doğru çözümü hiç bir yöntem garanti etmemekle birlikte, açıklanan yöntemin standart test fonksiyonlarında başarıya ulaştığı görülmüştür. Burada önerilen yöntem kontrol kuramının global optimizasyon probleminin çözümüne yeni bir yaklaşım ve bakış açısı getirmektedir.
[1] GUSTAFSSON Kjell, Step size control in ordinary differential equations, Lund Institute of Technology , Sweden, 1988
[2] TÖRN Aimo, ZILINSKAS Antanas, Global optimization, Lecture notes in computer science, Berlin , 1988
[3] QIN Joe, BORDERS Guy, A multiregion controller for nonlinear process control, IEEE
Transactions on fuzzy systems , February 1994
[4] MAMDANI E.H., An experiment in linguistic synthesis with a fuzzy logic controller, Int.J. Man-machine studies, vol. 7, pp.1-13, 1975
[5] ZHIGLJAVSKY Anatoly, Theory of global random search, Kluwer academic publishers, 1991
EK 1:
Tek değişken için bulanık kontrolör ü ile global optimizasyon algoritması